Loopholers Anonymous - a wretched hive of scum and villainy

Milchcow wrote:
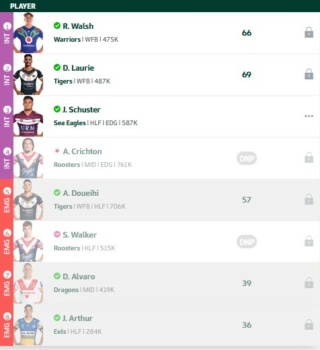
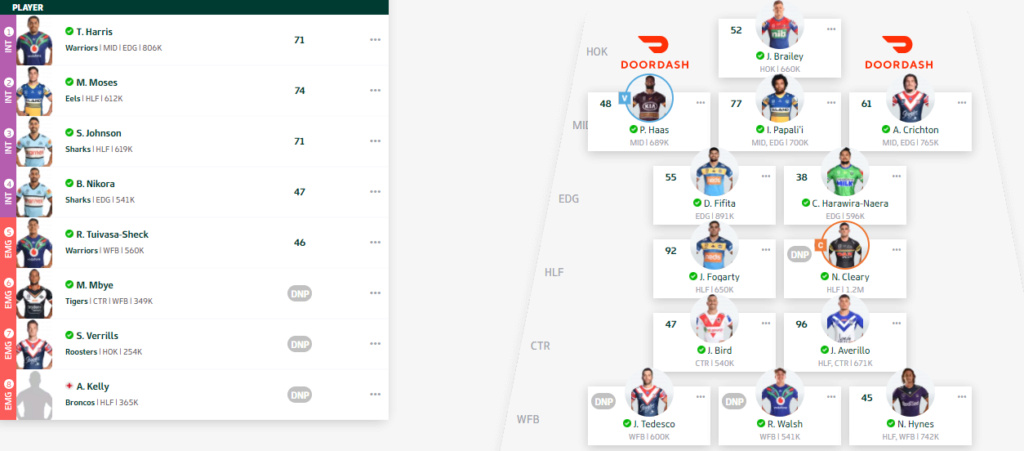
Only a WFB can come in for a starting WFB

You have no playing WFBs in your 14-21 so no one available to come in for Teddy
Opponent had Reimiss Smith sub for Teddy and Brodie Jones come up into the 17 to replace Smith

DAMN IT! haha thanks mate. Appreciate it.

The loops are in overdrive this week. Was going to try wrangle 3 with Leniu out too, but two with Avo and Walsh will do

Crichton
Schuster
Avo
Walsh

Walker
Simpkin
Uto
Leniu

Looks right? If Walker goes good leave as is, if not move the others up? I wonder if I'm looping the wrong player though, but gotta have faith in someone

Here's what I'm thinking. Walker to Hynes for first trade. Second trade I can hold if one of Laurie or Alvaro puts up a decent score. Someone want to check my loops?

Watson
Haas TPJ Peachey
Schuster Matterson
Cleary Moses
Burton Bird
Teddy Turbo Walsh

Fogarty
Koroisau
Hynes
Brailey

Laurie
Alvaro
Crichton
Simpkin

Laurie and Alvaro play at the same time. If Alvaro scores well leave it as it is a he comes in for Peachey. If Laurie scores better, then swap Brailey and Watson and then Watson with Peachey and I get Laurie's score. If both score poorly I then have the option of trading Crichton to a player in any position that plays after Friday night (JFH for example, haven't thought that far yet)

Thoughts?

Mulvy wrote:Here's what I'm thinking. Walker to Hynes for first trade. Second trade I can hold if one of Laurie or Alvaro puts up a decent score. Someone want to check my loops?

Watson
Haas TPJ Peachey
Schuster Matterson
Cleary Moses
Burton Bird
Teddy Turbo Walsh

Fogarty
Koroisau
Hynes
Brailey

Laurie
Alvaro
Crichton
Simpkin

Laurie and Alvaro play at the same time. If Alvaro scores well leave it as it is a he comes in for Peachey. If Laurie scores better, then swap Brailey and Watson and then Watson with Peachey and I get Laurie's score. If both score poorly I then have the option of trading Crichton to a player in any position that plays after Friday night (JFH for example, haven't thought that far yet)

Thoughts?

Looks right to me - impressed with the use of Watson and Peachey's DPPs. Now off to look at my team...

Mulvy wrote:Here's what I'm thinking. Walker to Hynes for first trade. Second trade I can hold if one of Laurie or Alvaro puts up a decent score. Someone want to check my loops?

Watson
Haas TPJ Peachey
Schuster Matterson
Cleary Moses
Burton Bird
Teddy Turbo Walsh

Fogarty
Koroisau
Hynes
Brailey

Laurie
Alvaro
Crichton
Simpkin

Laurie and Alvaro play at the same time. If Alvaro scores well leave it as it is a he comes in for Peachey. If Laurie scores better, then swap Brailey and Watson and then Watson with Peachey and I get Laurie's score. If both score poorly I then have the option of trading Crichton to a player in any position that plays after Friday night (JFH for example, haven't thought that far yet)

Thoughts?

That's A+ looping right there using Brailey and Watson that way, doubt I would've thought of that. Definitely will work as you say.

When you say you can trade someone in for Crichton if both Alvaro and Laurie score poorly, you wouldn't be able to avoid taking one of Alvaro or Laurie's score though right?

BCT05 wrote:

That's A+ looping right there using Brailey and Watson that way, doubt I would've thought of that. Definitely will work as you say.

When you say you can trade someone in for Crichton if both Alvaro and Laurie score poorly, you wouldn't be able to avoid taking one of Alvaro or Laurie's score though right?

I believe I could swap Brailey back to hooker, Watson to Mid, Peachey to INT so that Crichton and Peachey can then be swapped right? All parties involved play after Friday so shoud be okay??

Thanks for the help fellas!

Mulvy wrote:

I believe I could swap Brailey back to hooker, Watson to Mid, Peachey to INT so that Crichton and Peachey can then be swapped right? All parties involved play after Friday so shoud be okay??

Ah yep I see, very nice

Can anyone see a double loop for me here.  I'm getting a little rusty trying to work something out.

Brailey
Haas Watson IPap
Matto Schuster
Cleary Fog
Bird Kelly
To'o Walsh Ted

Moses Laurie Alvaro Walker

Crichton Peachey Simo Leniu

Anyway to double loop?

If I have Teddy, Hynes, Papy in my WFB

and Walsh in my 19 and Laurie as my 20 that will bring one of them in right?

Have a pretty average one this week. S.Walker and Watson in the loop using Peachey

Honeysett wrote:If I have Teddy, Hynes, Papy in my WFB

and Walsh in my 19 and Laurie as my 20 that will bring one of them in right?

You get Walsh's score, unless you have a WFB in your 14-18.

wolfking wrote:Can anyone see a double loop for me here.  I'm getting a little rusty trying to work something out.

Brailey
Haas Watson IPap
Matto Schuster
Cleary Fog
Bird Kelly
To'o Walsh Ted

Moses Laurie Alvaro Walker

Crichton Peachey Simo Leniu

Anyway to double loop?

All I could come up with is Alvaro at 18 and Leniu at 19. Both being MID's make it impossible to loop Leniu with say Simo and Alvaro with say Walker I believe. Will double loop and can take Alvaro's score and play Simo or Walker or if leniu does well too then can take both their scores or play both Simo and Leniu. If Leniu kills it and Alvaro does shit then there's nothing I can do.

Hi Team, can someone please explain what happens here? My old brain cant work it out but I think I will get Doueihi & Alvaro's scores if Schuster is out?

Yes

Am I able to loop here?

Ideally want RTS in the loop, so if he plays FB i'll play but him but if he's wing he will be #18... otherwise probably gamble him or Nikora out.

bigbruno wrote:Am I able to loop here?

Ideally want RTS in the loop, so if he plays FB i'll play but him but if he's wing he will be #18... otherwise probably gamble him or Nikora out.

I believe you can't loop your WFB's because you would need a red dot at WFB. You could use Kelly for your bench but he plays first. However being sneaky, you could put Kelly at HLF, but that doesn't work either because there are other halfs on the bench. Don't think you can loop mate unless there's a really creative one I can't think of.

Cheers lads figured as much.. damnit.